从严格的数学角度下分析时间复杂度的计算方法

预备知识：

①积分近似：

$$\sum_{i=0}^nf(i)\sim\int_{i=0}^{i=n}f(i) di$$

​ 一般地：

$$\sum_{i=0}^nf(i)\le\int_{i=0}^{i=n}f(i) di$$

②分治递归式通解：（主定理的原式）

$$T(n)=aT(n/b)+f(n)$$

​ 通解为：

$$T(n)=\Theta(n^{\log_ba})+ \sum_{i=0}^{\lceil\log_bn\rceil}a^if(n/b^i)$$

​ 其中$\lceil\log_bn\rceil=[\log_bn]-1$，求和部分直接用积分近似计算即可

③衡量算法效率参数

衡量算法效率参数	数学语言	表示
大$O$法	$f(n)\le cg(n)$	$O(g(n))$
大$\Theta$法	$c_1g(n)\le f(n)\le c_2g(n)$	$\Theta(g(n))$
大$\Omega$法	$f(n)\ge cg(n)$	$\Omega(g(n))$
近似法	$\lim_{i\to0}=f(n)/g(n)=1$	$\sim g(n)$

其中大$O$法和大$\Omega$法，常用于时间复杂度的标度。一般来说，时间复杂度用$O$。

for循环

①循环嵌套，变量间无关联

for(int i = 0; i < n; i++)
	for(int j = 0; j < n; j++)
		...

​ 用求和表示：

$$T(n)=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}1$$

​ 计算时间复杂度：

​ 法①：

$$T(n)=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}1=\sum_{i=0}^{n-1}(n-1-0+1)=n\sum_{i=0}^{n-1}1=n^2$$

​ 法②：

$$T(n)=\sum_{i=0}^{n-1}\sum_{j=0}^{n-1}1\le\iint didj=\int_{i=0}^{i=n-1}di\int_{j=0}^{j=n-1}dj=n^2$$

​ 故时间复杂度为$O(n^2)$

②嵌套循环，变量间有关联

for(int i = 0; i < n; i++)
	for(int j = i + 1; j < n; j++)
		...

​ 用求和表示：

$$T(n)=\sum_{i=0}^{n-1}\sum_{j=i+1}^{n-1}1$$

​ 计算时间复杂度

​ 法①：

$$T(n)=\sum_{i=0}^{n-1}\sum_{j=i+1}^{n-1}1=\sum_{i=0}^{n-1}(n-i-1)=n^2/2-n/2=O(n^2)$$

​ 法②：

$$T(n)=\sum_{i=0}^{n-1}\sum_{j=i+1}^{n-1}1\sim\iint didj=\int_{i=0}^{i=n-1}di\int_{j=i+1}^{j=n-1}dj=\int_{i=0}^{i=n-1}(n-i-1)di=n^2-\frac{i^2}{2}|_0^{n-1}-n\\ =n^2/2-1/2=O(n^2)$$

​ 在这里可以发现积分的结果一般比离散求和要大，这保证了时间上界，所以积分近似有效且高效。

​ 故时间复杂度为$O(n^2)$

while循环（假设$i$从1开始变化）

①条件变量呈线性变化

​ 直接用for循环的方法即可，但如果增量不为1的话：

while(i <= n){
	i += 2;
    ...
}

​ $i$的变化看作是等差数列

$$1\ 3\ 5\ ...\ n$$

​ 那么上述数列有多少项数，那么耗时就为多少：

​ 先写出数列的递归表达式：

$$x(k)=x(k-1)+2$$

​ 计算得出：

$$x(k)=2k-1$$

​ 令$x(k)=n$，这个时候$k=T(n)$

$$T(n)=k=\frac{n+1}{2}= O(n)$$

​ 时间复杂度为$O(n)$

②条件变量呈k次变化

while(i <= n){    
	i *= 2;
    ...
}

​ $i$变量每次乘以2，同样可以看成数列，但这个时候$i$的变化为等比数列：

$$1\ 2\ 4\ ...\ n$$

​ 同样的，令数列：

$$x(k)=2\ x(k-1)$$

​ 计算得出：

$$x(k)=2^{k-1}$$

​ 令$x(k)=n$，这个时候$k=T(n)$

$$T(n)=k=\log n+1= O(\log n)$$

​ 时间复杂度为$O(\log n)$

递归式求解

对于递归式，只要求出方程就可以了，一般来说难度不大，下面介绍典型递归式。

线性递归

形如

$$T(n)=aT(n-b)+f(n)$$

一般采用数列不动点求出方程

比如

$$T(n)=T(n-1)+n$$

求得

$$T(n)=O(n^2)$$

比如

$$T(n)=2T(n-1)+n$$

求得数列不动点$x=-n$，构造：

$$T(n)-x=2T(n-1)+n-x$$

不难得到：

$$T(n)+n=2[T(n-1)+n]$$

求得：

$$T(n)=O(2^n)$$

什么是数列不动点？

对于一阶线性递推数列：

$$x_n=px_{n-1}+q$$

令$xn=x{n-1}=x$，这个$x$就是不动点：

$$x=\frac{q}{1-p}$$

因此：

$$x_n-x=px_{n-1}+q-x$$

化简得到：

$$x_n-\frac{q}{1-p}=p(x_{n-1}-\frac{q}{1-p})$$

分治递归

常见的分治递归有如下的表达式：

$$T(n)=aT(n/b)+f(n)$$

不难证明出通解为：

$$T(n)=\Theta(n^{\log_ba})+ \sum_{i=0}^{\lceil\log_bn\rceil}a^if(n/b^i)$$

其中$\lceil\log_bn\rceil=\log_bn-1$，求和部分直接用积分近似计算即可。

但这还是麻烦点，所以有人通过这个通解总结出了分治递归的主定理方法：

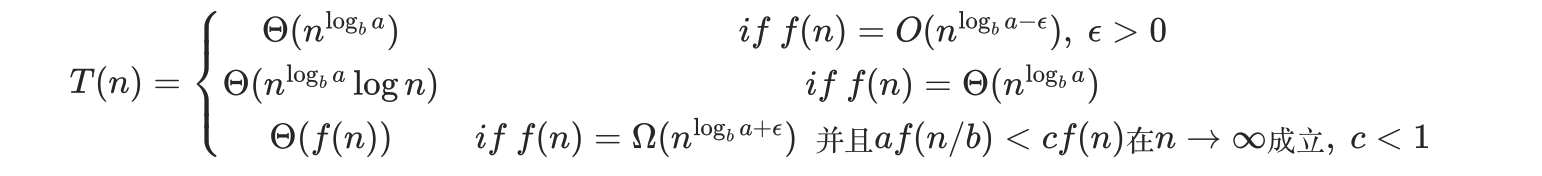
复杂的分治递归需要用到换元法等知识，比如求解：

$$T(n)=2T(\sqrt n)+1$$

这时候我们需要对这个式子进行变式：

令$n=2^m$，于是：

$$T(2^m)=2T(2^{m/2})+1$$

令$P(m)=T(2^m)$，那么

$$P(m)=2P(m/2)+1$$

这个时候就好解决了，可以求出来这个递归式的时间复杂度为$O(m)$（属于主定理的第一种情况，$n^{log_ba}=n^1$，并且$f(n)=1=n^0=O(n^{1-\epsilon})，当$$0<\epsilon \le1$成立）

换元回来就得到：$O(\log n)$

总结

​ 时间复杂度不难分析，只需要观察代码，然后分析是啥变量在变化，条件是啥。然后用数列表示出这个变量，那么这个数列的项数就是时间函数，求出时间函数一切都好办辣！

​ 对于增量不为1的情况，还是构造数列$x(k)$，解出$x(T(n))=n$这个方程就可以了！