投影矩阵的具体推导

正交投影

正交投影的步骤是先平移到世界原点，然后进行缩放，把视界体缩放成长度为2的正方体，取值为$[-1,1]^3$:

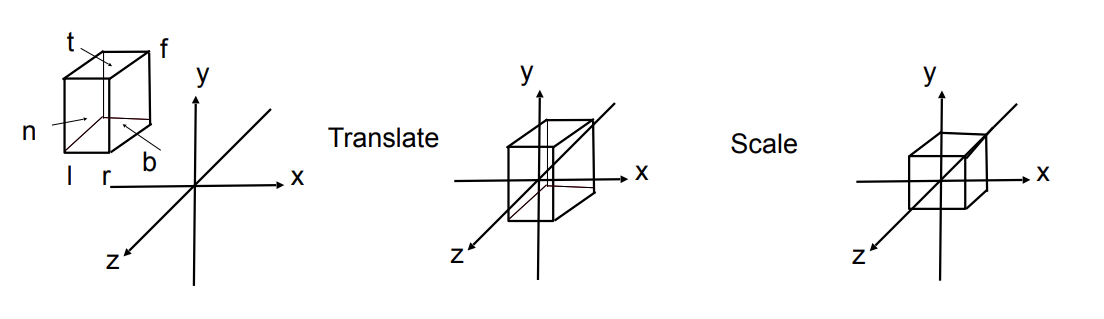
左极端点为$(left,bottom,-near)$，右极端点为$(right,top,-far)$

用矩阵变换描述上述过程：

$$M_{ortho}=ST$$

其中，平移的时候，应当让视见体的中心$\left(
\frac{right+left}{2},
\frac{top+bottom}{2},
-\frac{near+far}{2}
\right)$移动到世界原点，于是平移矩阵如下：

$$T= \left[ \begin{matrix} 1 & 0 & 0 & -\frac{l+r}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & \frac{n+f}{2}\\ 0 & 0 & 0 & 1 \end{matrix} \right]$$

然后进行放缩，将长度为$right-left,top-bottom,near-far$的长宽高的视界体放缩为长宽高均为2的正方体$[-1,1]^3$。

显然，放缩矩阵为：

$$S=\left[ \begin{matrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right]$$

因此：

$$\begin{aligned} M_{ortho}=ST&= \left[ \begin{matrix} \frac{2}{r-l} & 0 & 0 & 0\\ 0 & \frac{2}{t-b} & 0 & 0\\ 0 & 0 & \frac{2}{n-f} & 0\\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} 1 & 0 & 0 & -\frac{l+r}{2}\\ 0 & 1 & 0 & -\frac{t+b}{2}\\ 0 & 0 & 1 & \frac{n+f}{2}\\ 0 & 0 & 0 & 1 \end{matrix} \right]\\ &= \left[ \begin{matrix} \frac{2}{r-l} & 0 & 0 & \frac{l+r}{l-r}\\ 0 & \frac{2}{t-b} & 0 & \frac{b+t}{b-t}\\ 0 & 0 & \frac{2}{n-f} & \frac{n+f}{n-f}\\ 0 & 0 & 0 & 1 \end{matrix} \right] \end{aligned}$$

透视投影

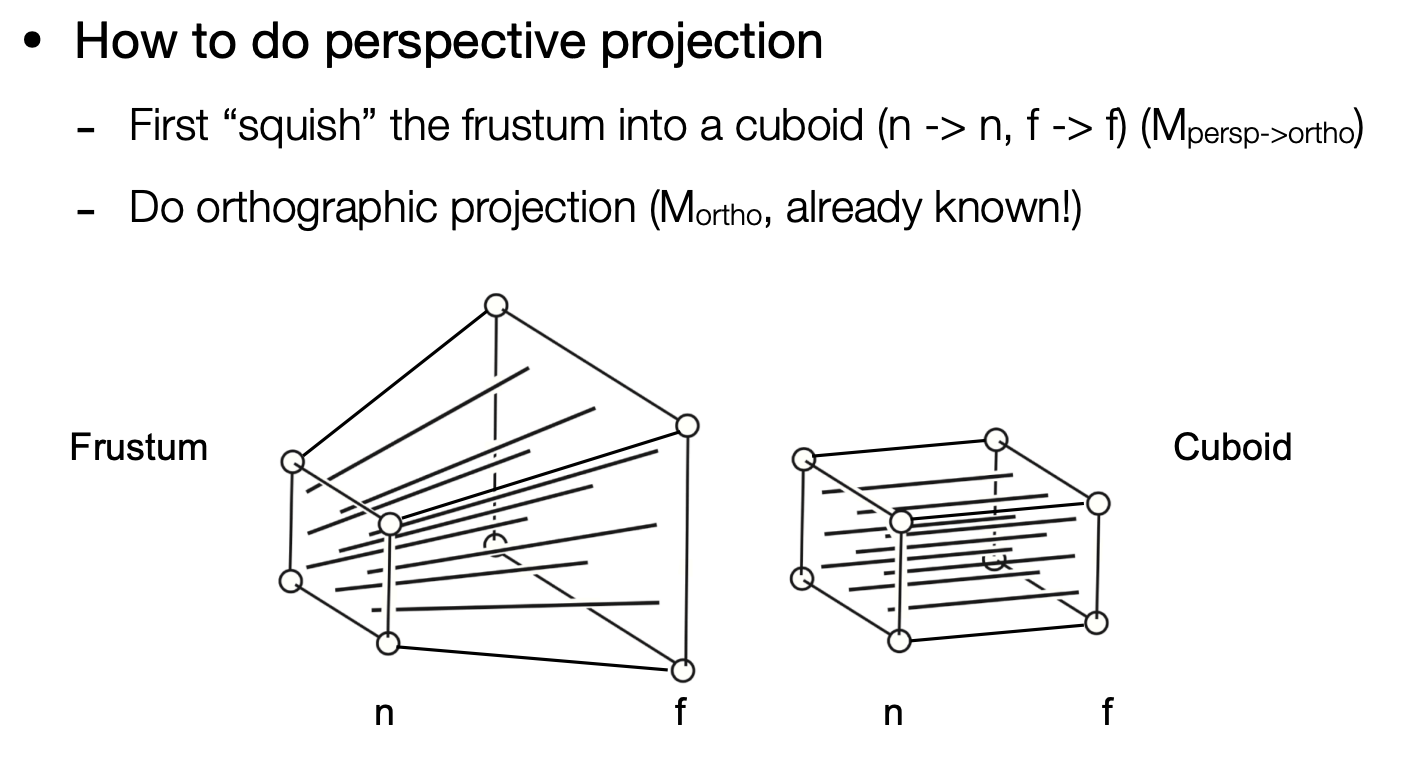
步骤为，先压扁，后正交：

$$M_{perspective}=M_{ortho}M_{p}$$

首先计算$M_p$，根据相似三角形：

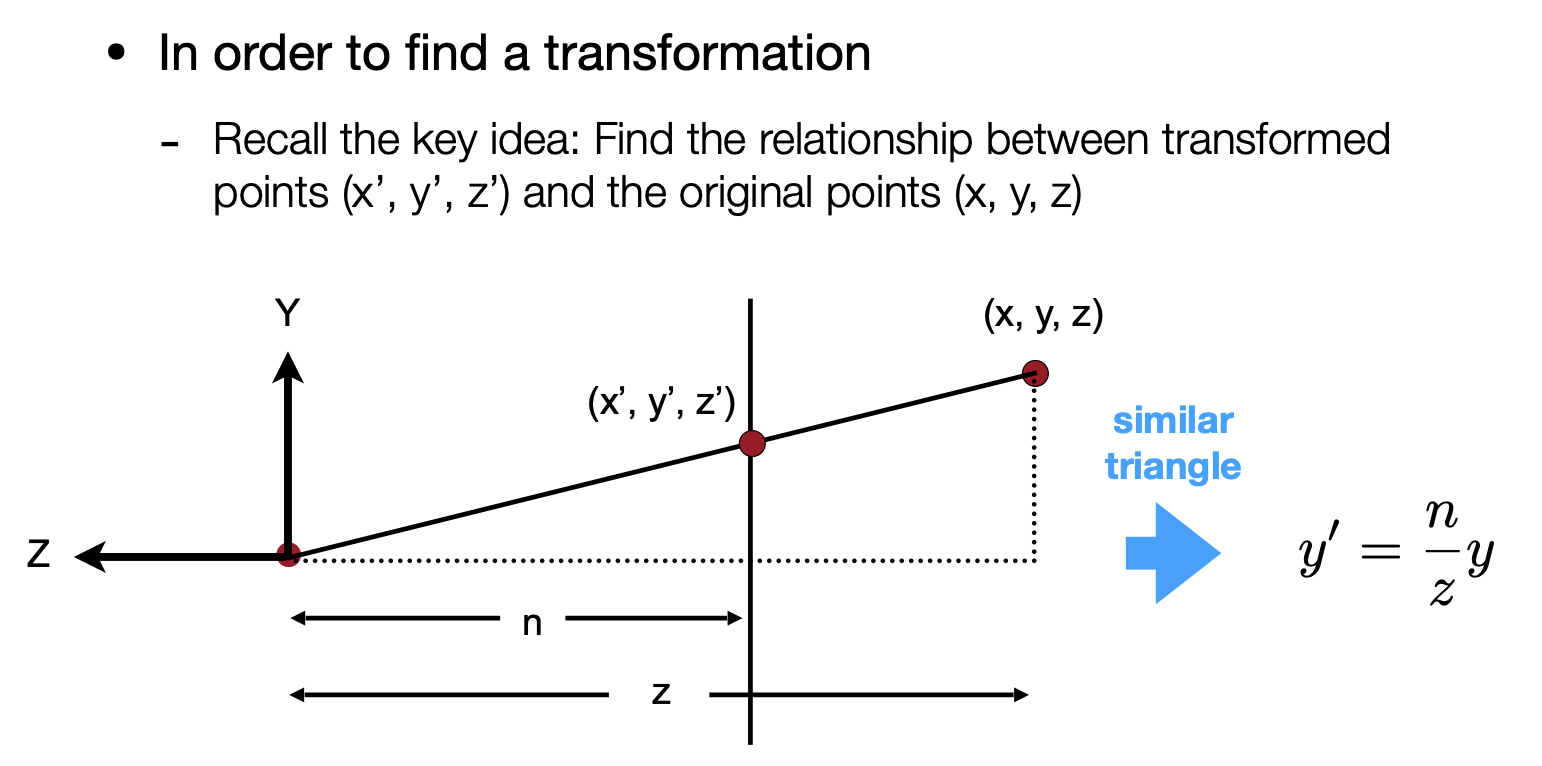
注意这里的n和z的实际值都是负值，n是near：

$$y'=\frac{-ny}{z},x'=\frac{-nx}{z}$$

这样就可以得到：

$$M_p \left[ \begin{aligned} x\\ y\\ z\\ 1 \end{aligned} \right] = \left[ \begin{aligned} nx\\ ny\\ ?\\ -z \end{aligned} \right]$$

不难得出：

$$M_p= \left[ \begin{matrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ ? & ? & ? & ?\\ 0 & 0 & -1 & 0 \end{matrix} \right]$$

为了求解完整的矩阵，可以参考透视投影矩阵的两个规则：

(1) 近平面内的所有坐标的z在变换后保持不变

(2) 远平面内的所有坐标的z在变换后保持不变

对于(1)而言，任意近平面的坐标为$\left[\begin{matrix}
x & y & -n & 1
\end{matrix}\right]$，那么：

$$M_p \left[ \begin{matrix} x\\ y\\ -n\\ 1 \end{matrix} \right] = \left[ \begin{matrix} nx\\ ny\\ -n^2\\ n \end{matrix} \right]$$

可以知道$M_P$的第三行为$\left[\begin{matrix}
0 & 0 & A & B
\end{matrix}\right]$，使得：

$$\left[\begin{matrix} 0 & 0 & A & B \end{matrix}\right] \left[ \begin{matrix} x\\ y\\ -n\\ 1 \end{matrix} \right] =-n^2$$

计算得出：

$$-An+B=-n^2$$

对于(2)而言，任意远平面的坐标为$\left[\begin{matrix}
x & y & -f & 1
\end{matrix}\right]$，那么：

$$M_p \left[ \begin{matrix} x\\ y\\ -f\\ 1 \end{matrix} \right] = \left[ \begin{matrix} fx\\ fy\\ -f^2\\ f \end{matrix} \right]$$

可以知道$M_P$的第三行为$\left[\begin{matrix}
0 & 0 & A & B
\end{matrix}\right]$，使得：

$$\left[\begin{matrix} 0 & 0 & A & B \end{matrix}\right] \left[ \begin{matrix} x\\ y\\ -f\\ 1 \end{matrix} \right] =-f^2$$

计算得出：

$$-Af+B=-f^2$$

联立方程组，解出：

$$\begin{aligned} A&=n+f\\ B&=nf \end{aligned}$$

所以：

$$M_p= \left[ \begin{matrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & nf\\ 0 & 0 & -1 & 0 \end{matrix} \right]$$

所以：

$$\begin{aligned} M_{perspective}=M_{ortho}M_{p}&= \left[ \begin{matrix} \frac{2}{r-l} & 0 & 0 & \frac{l+r}{l-r}\\ 0 & \frac{2}{t-b} & 0 & \frac{b+t}{b-t}\\ 0 & 0 & \frac{2}{n-f} & \frac{n+f}{n-f}\\ 0 & 0 & 0 & 1 \end{matrix} \right] \left[ \begin{matrix} n & 0 & 0 & 0\\ 0 & n & 0 & 0\\ 0 & 0 & n+f & nf\\ 0 & 0 & -1 & 0 \end{matrix} \right] \\ &= \left[ \begin{matrix} \frac{2n}{r-l} & 0 & \frac{r+l}{r-l} & 0\\ 0 & \frac{2n}{t-b} & \frac{t+b}{t-b} & 0\\ 0 & 0 & \frac{n+f}{n-f} & \frac{2nf}{n-f}\\ 0 & 0 & -1 & 0 \end{matrix} \right] \end{aligned}$$

简化透视投影矩阵

上面的透视投影矩阵推导是基于视见体函数的推导：

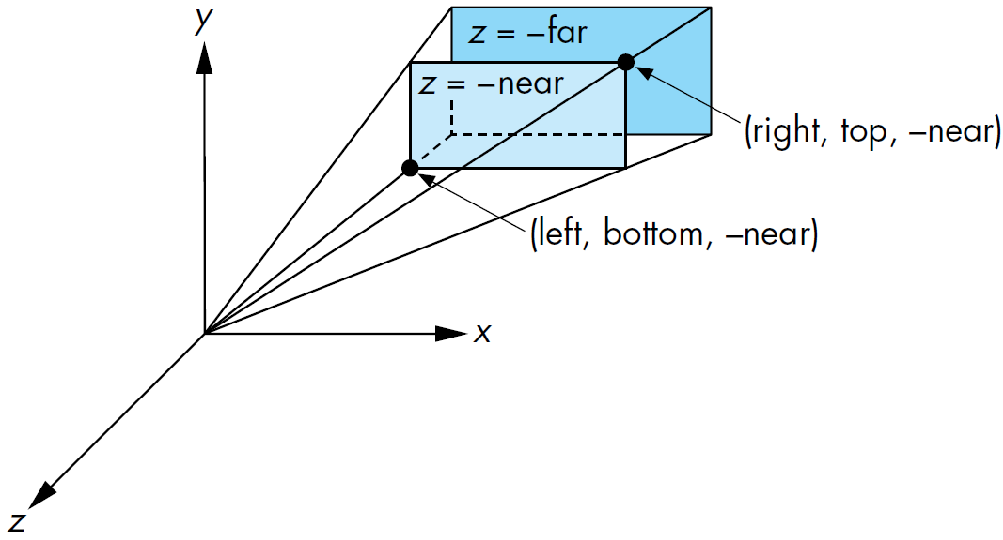
我们可以使用转换成基于透视函数的推导（消除$left,right,bottom,top$）：

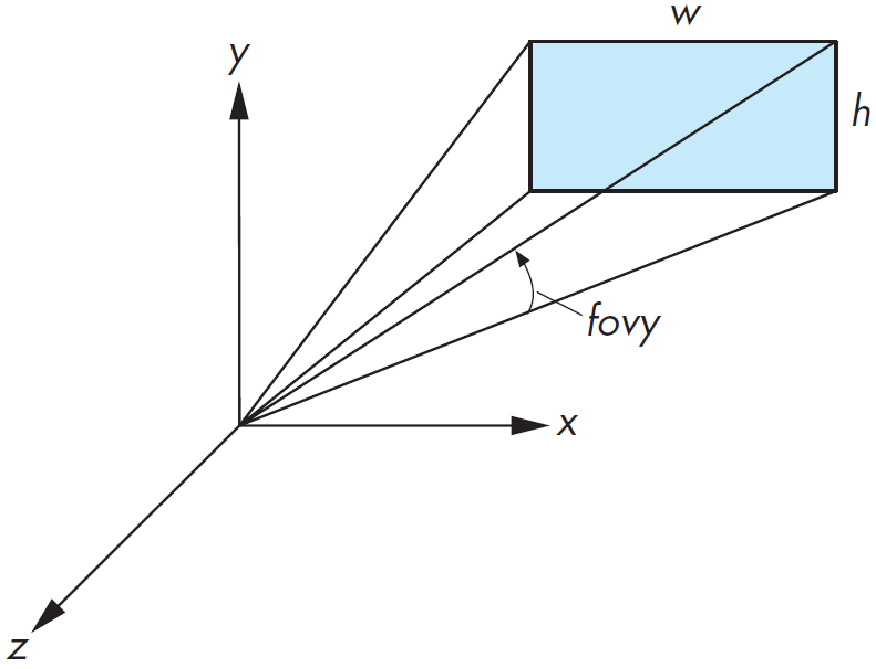
只需要将视见体函数的参数修改为标准对称的视见体：

$$\begin{aligned} &left=-right\\ &bottom=-top\\ &\tan(fov/2)=\frac{top}{near}\\ &aspect=\frac{2\times right}{2\times top}=\frac{right}{top} \end{aligned}$$

$fov$ 为视场角，$aspect$ 是宽长比，一般为窗口的宽长比值：

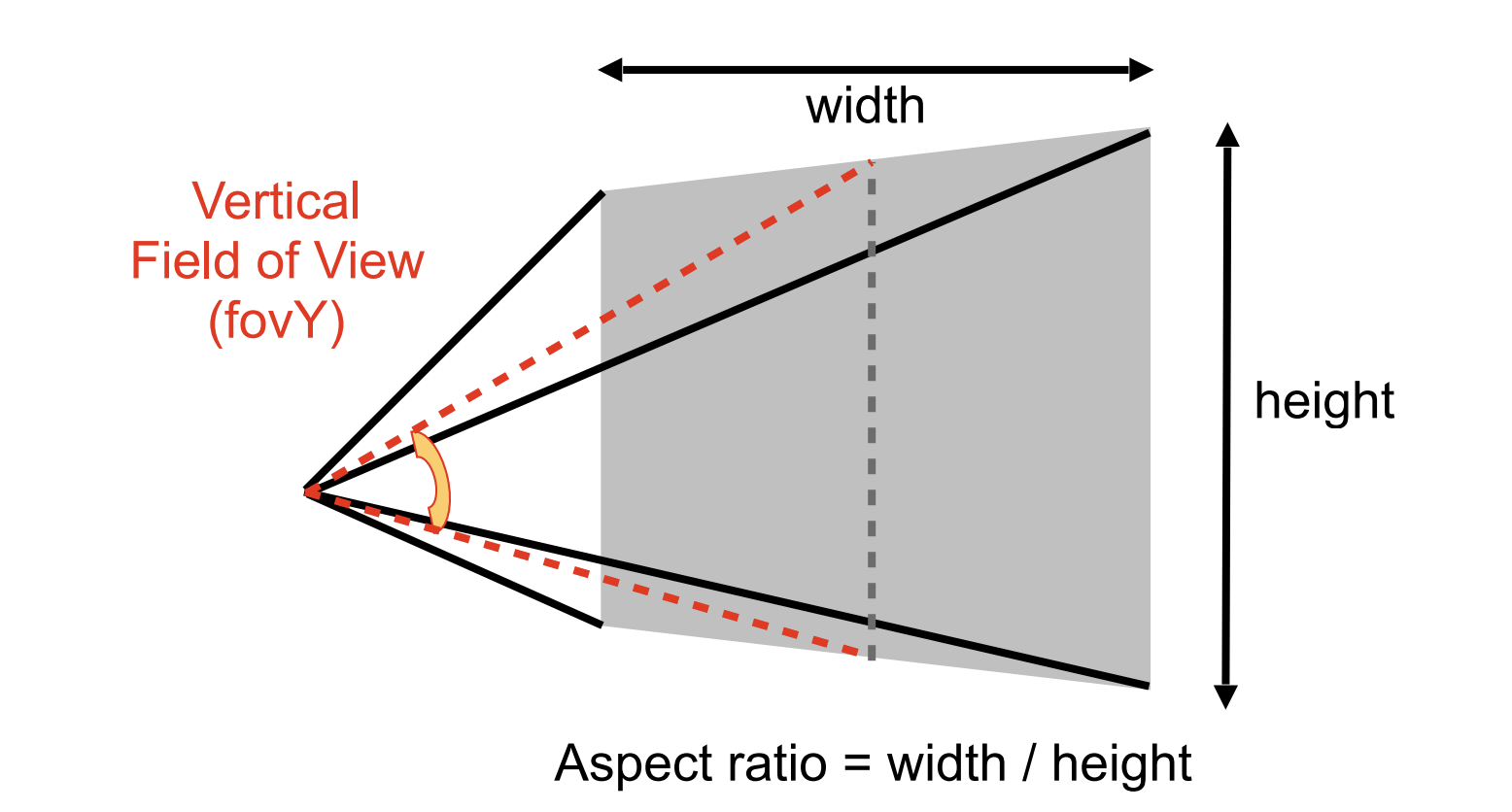
这样透视投影矩阵就可以简化成：

$$\begin{aligned} M_{perspective}&= \left[ \begin{matrix} \frac{n}{r} & 0 & 0 & 0\\ 0 & \frac{n}{t} & 0 & 0\\ 0 & 0 & \frac{n+f}{n-f} & \frac{2nf}{n-f}\\ 0 & 0 & -1 & 0 \end{matrix} \right] \end{aligned}$$

又因为：

$$\begin{aligned} \frac{n}{r}&=\frac{1}{\tan(fov/2)\frac{r}{t}}=\frac{1}{\tan(fov/2)\times aspect}\\ \frac{n}{t}&=\frac{1}{\tan(fov/2)} \end{aligned}$$

所以进一步得到最简形式：

$$\begin{aligned} M_{perspective}&= \left[ \begin{matrix} \frac{1}{\tan(fov/2)\times aspect} & 0 & 0 & 0\\ 0 & \frac{1}{\tan(fov/2)} & 0 & 0\\ 0 & 0 & \frac{n+f}{n-f} & \frac{2nf}{n-f}\\ 0 & 0 & -1 & 0 \end{matrix} \right] \end{aligned}$$

投影矩阵的具体推导

http://blog.inverseda.top/2023/03/17/ComputerGraphics/投影矩阵的具体推导/

Author

InverseDa

Posted on

2023-03-17

Updated on

2023-03-30

Licensed under

#数学计算机图形学投影矩阵线性代数